1
Machine Learning for Design
Lecture 8
Design and Develop Machine Learning Models - Part 2
2
ML Algorithms on Structured Data
3
Decision Trees
- Trained with labelled data (supervised learning)
- classes —> classification
- values —> regression
- Simple model that resembles human reasoning:
- Answering a lot of yes/no questions based on feature values
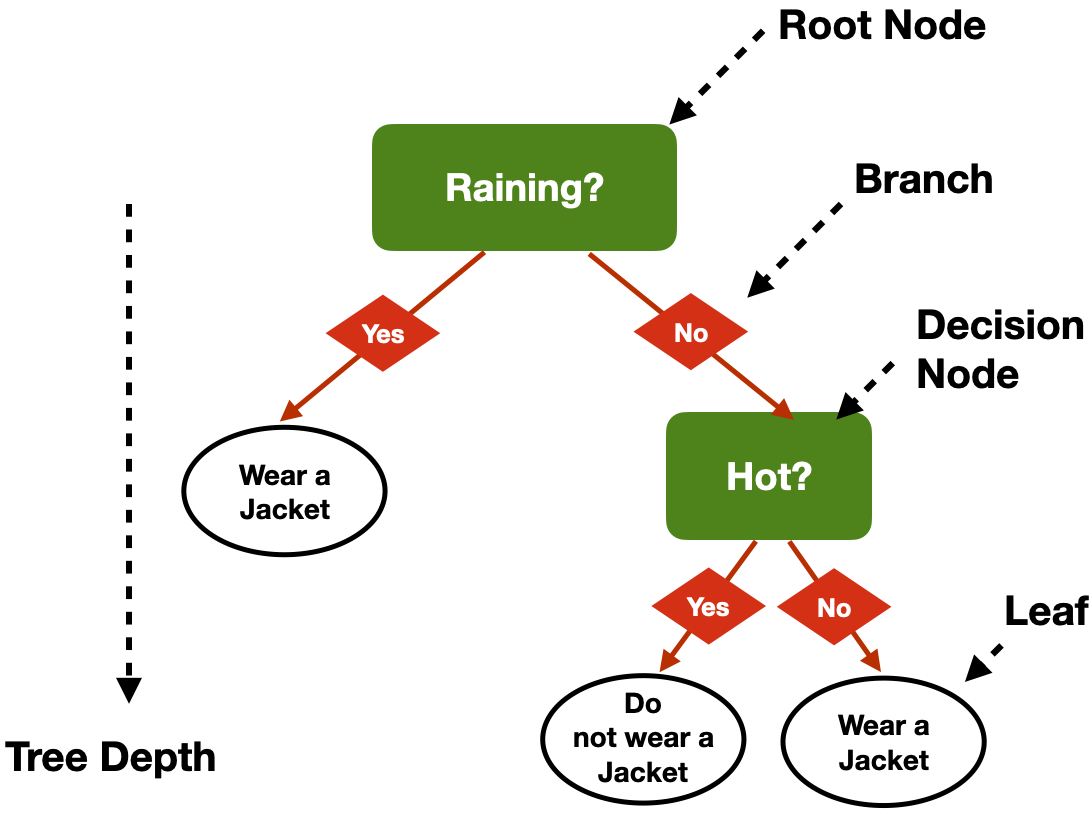
4
Problems
- Which questions to answer?
- How many questions? (Tree depth)
- In which order?
5
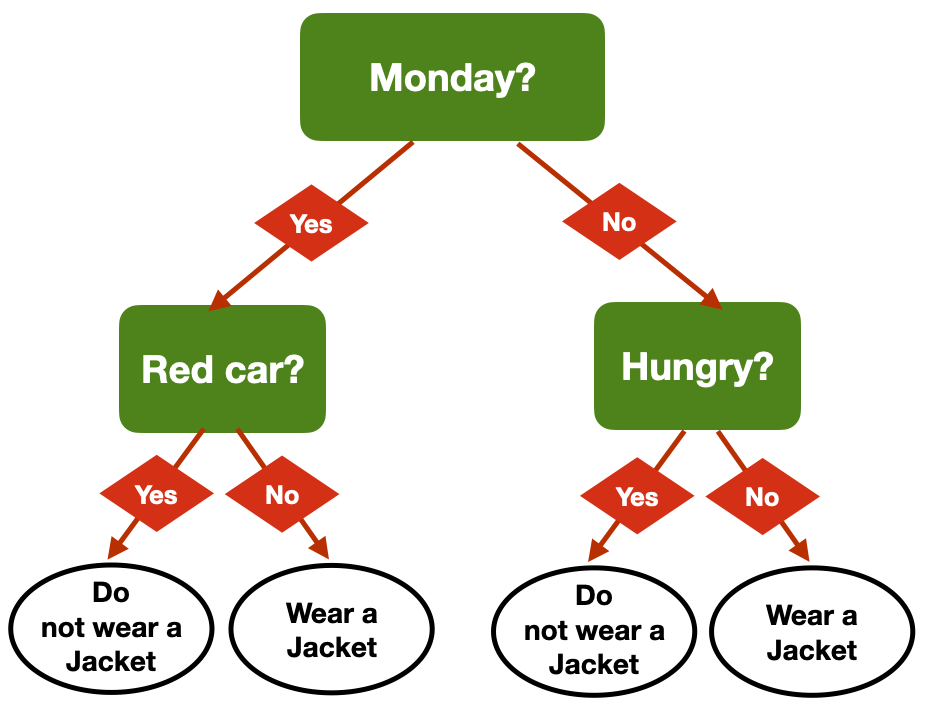
Same Problem, Multiple Trees
- Am I hungry?
- Is there a red car outside?
- Is it Monday?
- Is it raining?
- Is it cold outside?

6
Same Problem, Multiple Trees
Am I hungry?Is there a red car outside?Is it Monday?- Is it raining?
- Is it cold outside?

7
Same Problem, Multiple Trees
Am I hungry?Is there a red car outside?Is it Monday?- Is it raining?
- Is it cold outside?
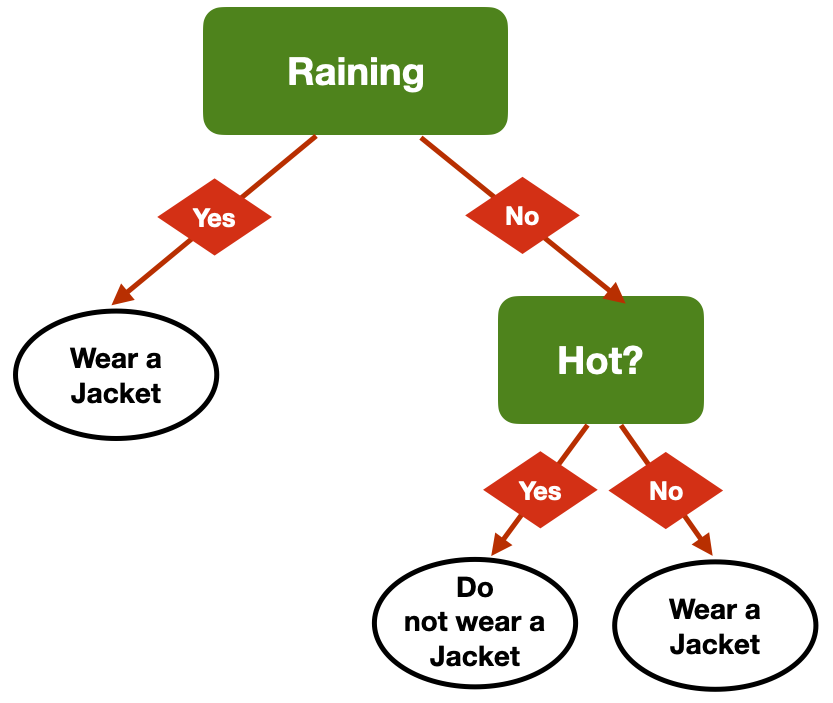
8
Same Decision, different tress


9
How to decide the best question to ask?
- Accuracy
- Which question helps me be correct more often?
- Gini Impurity Index
- A measure of diversity in a dataset —> diversity of classes in a given leaf node
- index = 0 means that all the items in a leaf node have the same class
- Which question helps me obtain the lowest average Gini impurity Index?
- A measure of diversity in a dataset —> diversity of classes in a given leaf node
- Entropy
- Another measure of diversity linked to information theory
- Which question helps me obtain the lowest average entropy?
10
Building the tree (pseudo-code)
- Add a root node, and associate it with the entire dataset
- This node has level 0. Call it a leaf node
- Repeat until the stopping conditions are met at every leaf node
- Pick one of the leaf nodes at the highest level
- Go through all the features, and select the one that splits the samples corresponding to that node in an optimal way, according to the selected metric.
- Associate that feature to the node
- This feature splits the dataset into two branches
- Create two new leaf nodes, one for each branch
- Associate the corresponding samples to each of the nodes
- If the stopping conditions allow a split, turn the node into a decision node, and add two new leaf nodes underneath it
- If the level of the node is i, the two new leaf nodes are at level i+1
- If the stopping conditions don’t allow a split, the node becomes a leaf node
- Associate the most common label among its samples
- That label is the prediction at the leaf
11
A geometrical perspective
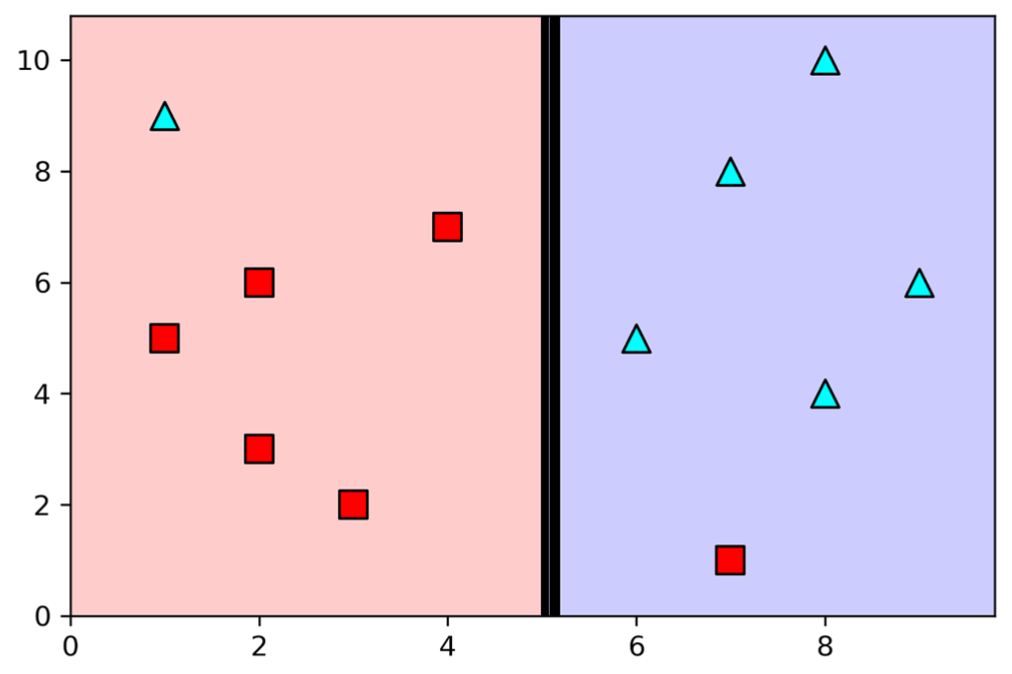
- Step 1 - Select the first question
- X>=5
- Best possible prediction accuracy with one feature
12
A geometrical perspective
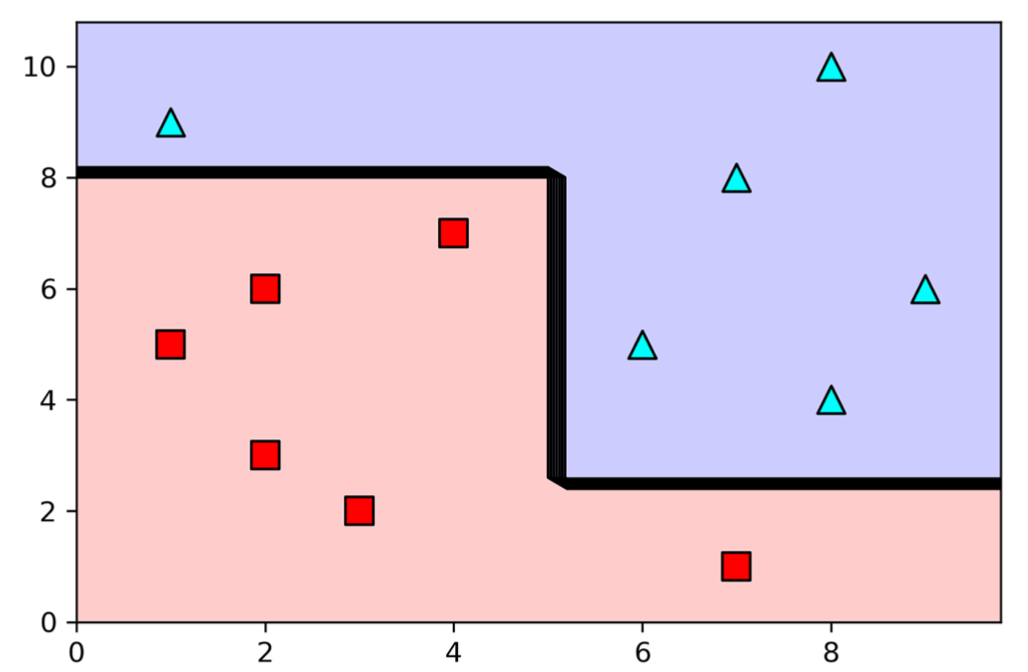
- Step 2 - Iterate
- x<5&y<8;
- x>=5&y>=2
- Perfect split of the feature space
13
Decision Trees: Pros
- Simple to understand and interpret.
- Trees can be visualized
- Requires little data preparation
- Other techniques often require data normalisation, dummy variables need to be created, and blank values need to be removed
- Able to handle both numerical and categorical data
14
Decision Trees: Cons
- Possible to create over-complex trees that do not generalize the data well
- overfitting
- Unstable —> small variations in the data might result in a completely different tree being generated
- Biased trees if some classes dominate
15
Ensemble Learning
Idea: combine several “weak” learners to build a strong learner
Random Forest: Weak learners are decision trees
16
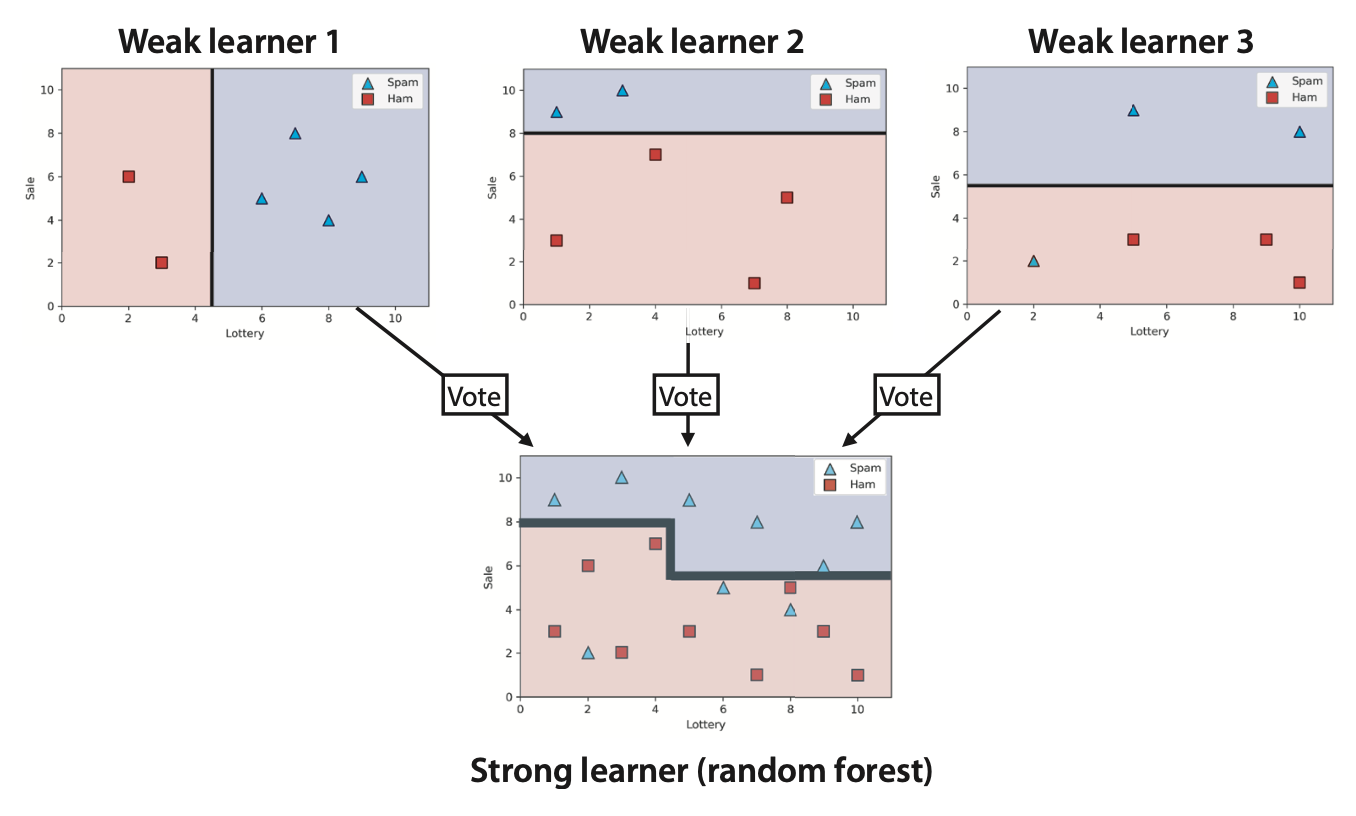
- Build random training sets from the dataset
- Train a different model on each of the sets
- weak learners
- Combination the weak models by voting (if it is a classification model) or averaging the predictions (if it is a regression model)
- For any input, each of the weak learners predicts a value
- The most common output (or the average) is the output of the strong learner
17
18
Clustering
19
What is clustering?
- Grouping items that “belong together” (i.e. have similar features)
- Unsupervised learning: we only use data features, not the labels\u2028
20
- We can detect patterns
- Group emails or search results
- Customer shopping patterns
- Regions of images
- Useful when you don’t know what you’re looking for
- But: can give you gibberish
- If the goal is classification, we can later ask a human to label each group (cluster)
21
Why do we cluster?
- Summarizing data
- Look at large amounts of data
- Represent a large continuous vector with the cluster number
- Counting
- Computing feature histograms
- Prediction
- Images in the same cluster may have the same labels
- Segmentation
- Separate the image into different regions
22
K-Means
- An iterative clustering algorithm
- Initialize: Pick K random points as cluster centres
- Alternate:
- Assign data points to the closest cluster centre
- Change the cluster centre to the average of its assigned points
- Stop when no points’ assignments change
23
24
Add 3 Centroids (randomly)
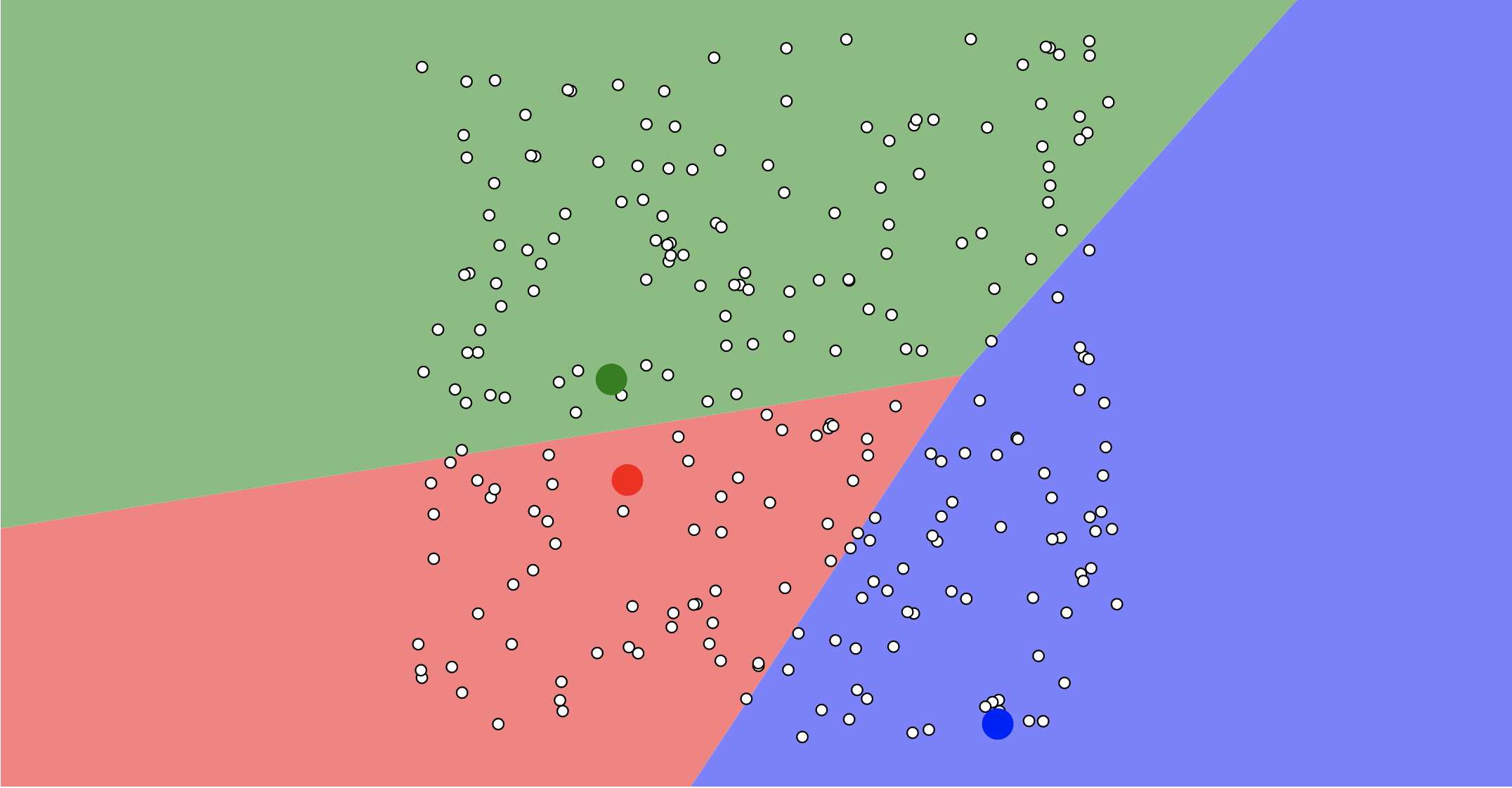
25
Assign Data Points
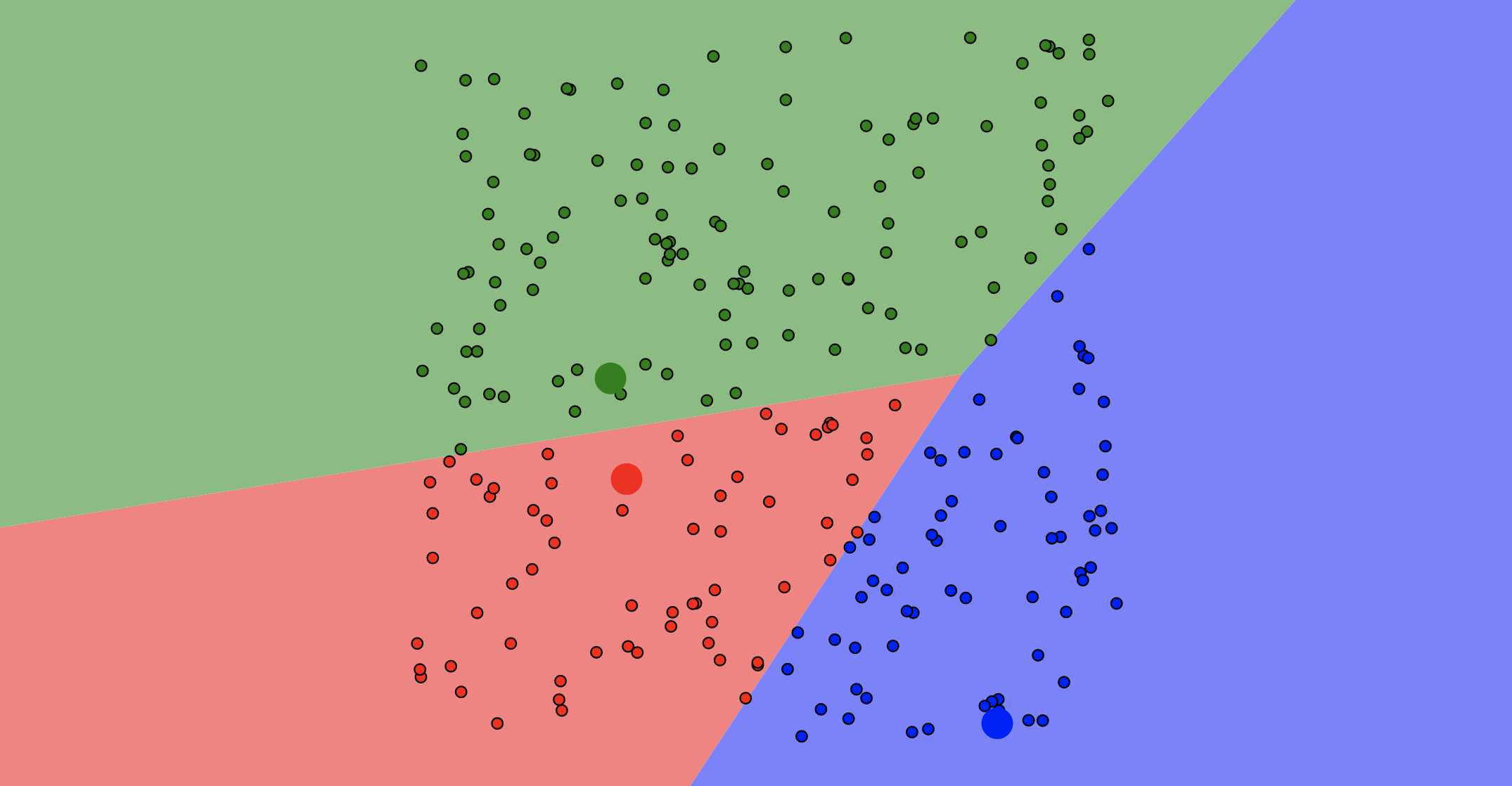
26
Update Centroids
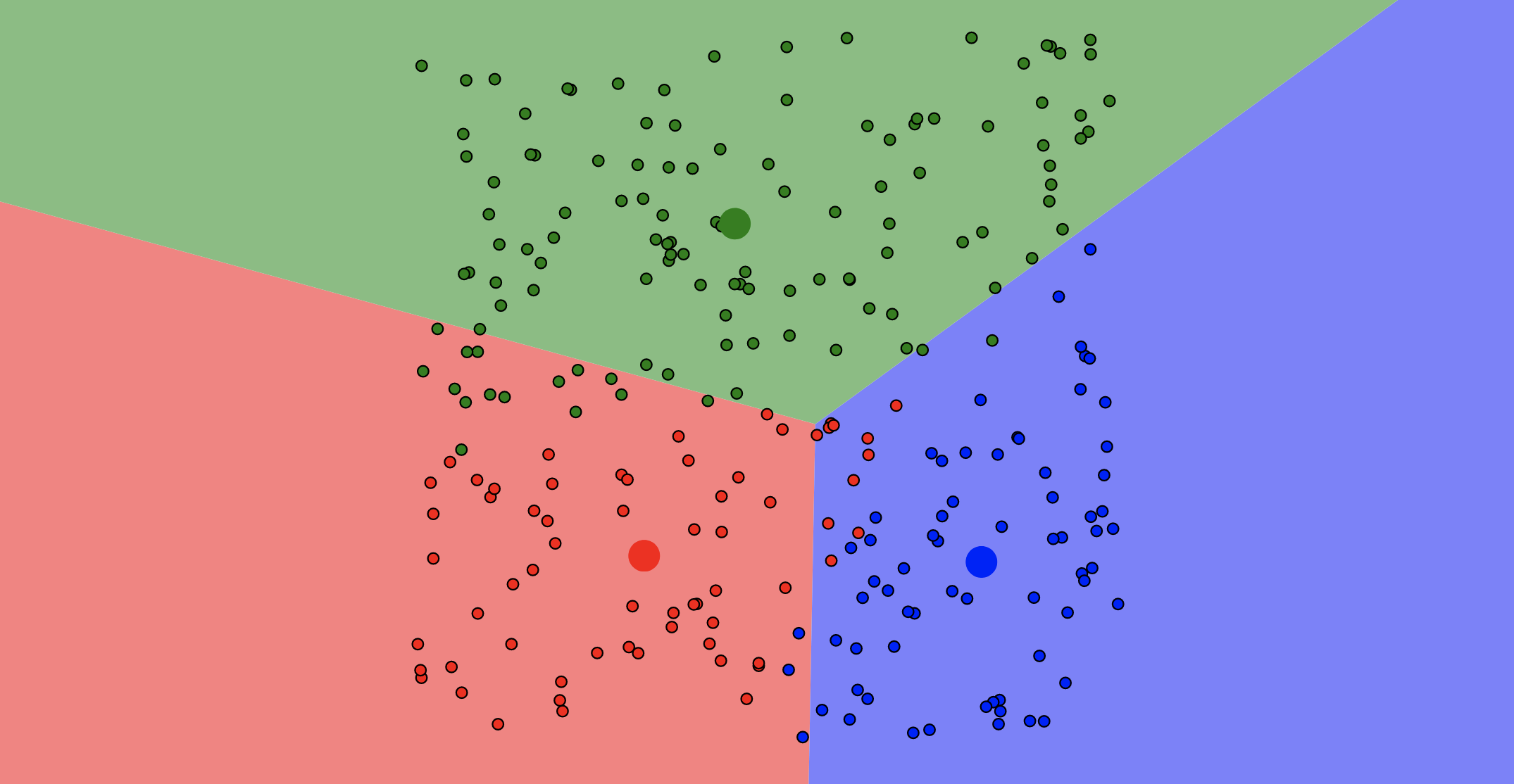
27
Re-Assign Data Points

28
Update Centroids

29
Re-Assign Data Points

30
Update Centroids

31
Re-Assign Data Points - Stop

32
Add 4 Centroids (randomly)

33
K-Means Pros
- Simple, fast to compute
- Guaranteed to converge in a finite number of iterations
34
K-Means Cons
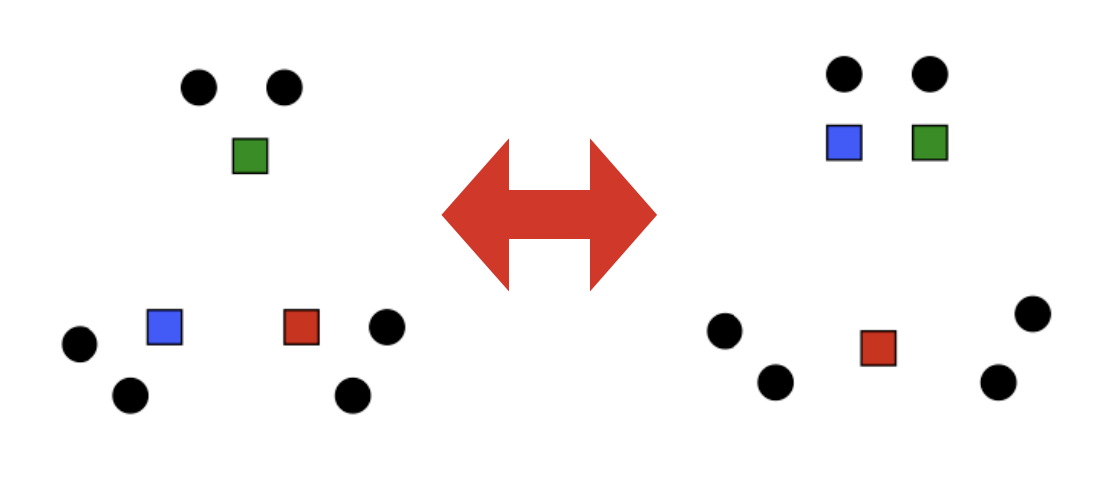
- Setting k?
- One way: silhouette coefficient
- Algorithm is heuristic
- It does matter what random points you pick!
- Sensitive to outliers
35
Example of K-means not working
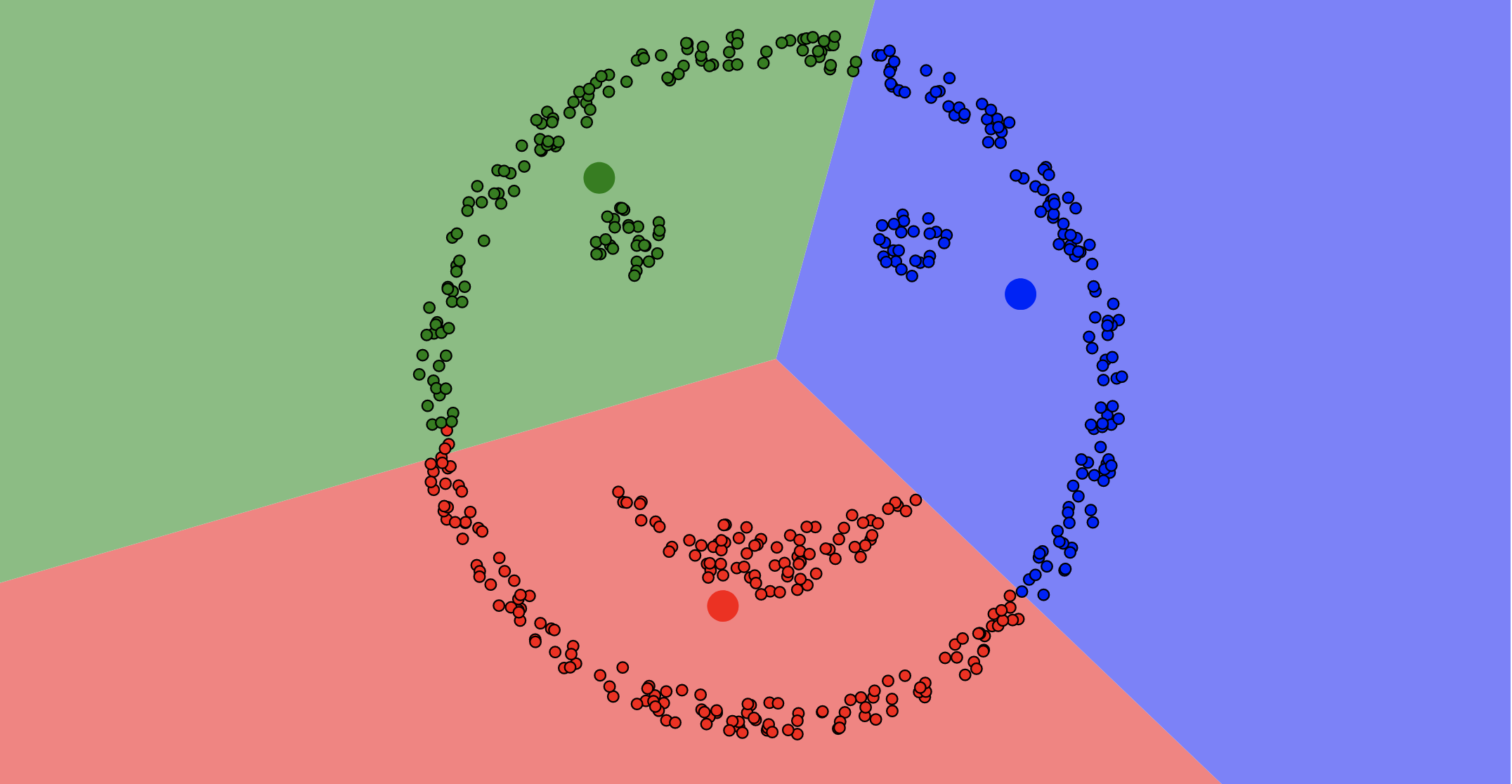
36
Back to Evaluation
37
- No free-lunch: there is no one best machine learning algorithm for all problems and datasets
- How well does a learned model generalize to a new evaluation set?
- Challenge: achieving good generalization and a small error
38
Underfitting vs. Overfitting
39
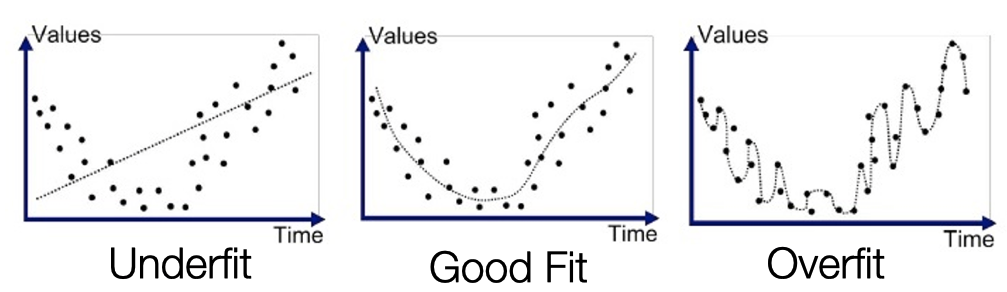
Regression
40
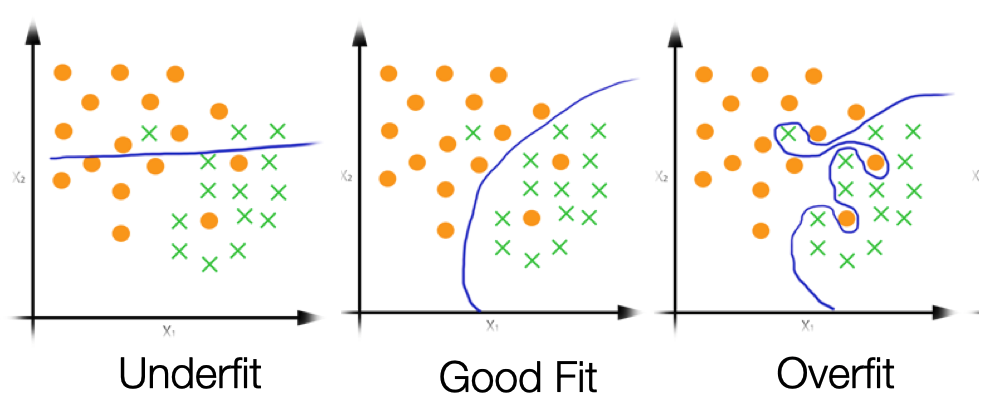
Classification
41
Components of expected loss
- Noise in data: unavoidable
- Bias: how much the average model differs from the true model
- Error due to inaccurate assumptions/simplifications made by the model
- Variance: how much models estimated from different training sets differ from each other
- Too much sensitivity to the samples
42
43
44
Protect Against overfitting
Low bias and high variance
Low training error and high test error
- The model
- is too complex
- matches too closely the idiosyncrasies (noise) of the training data
45
Protect Against underfitting
High bias and low variance
High training error and high test error
- The model
- is too simple
- does not adequately capture the patterns in the training data
46
47
Tuning Hyper-parameters
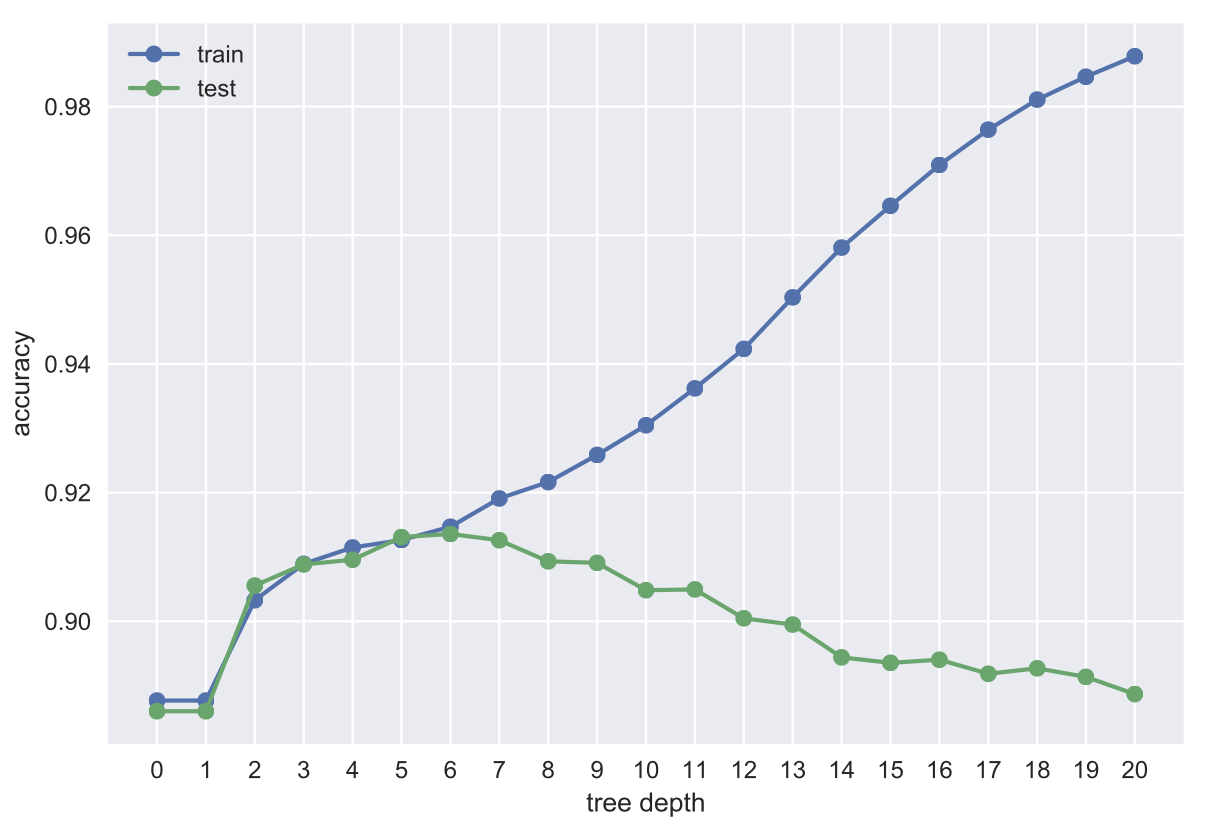
- Hyper-parameter: Inputs to the learning algorithms that control their behavior
- Examples:
- maximum tree depth in decision trees
- number of neighbors k in k-nearest neighbor
- Neural networks: architecture, learning rate
48
Tuning Hyper-parameters
- For a model to work well, they often need to be tuned carefully
- Huge search space! may be inefficient to search exhaustively
49
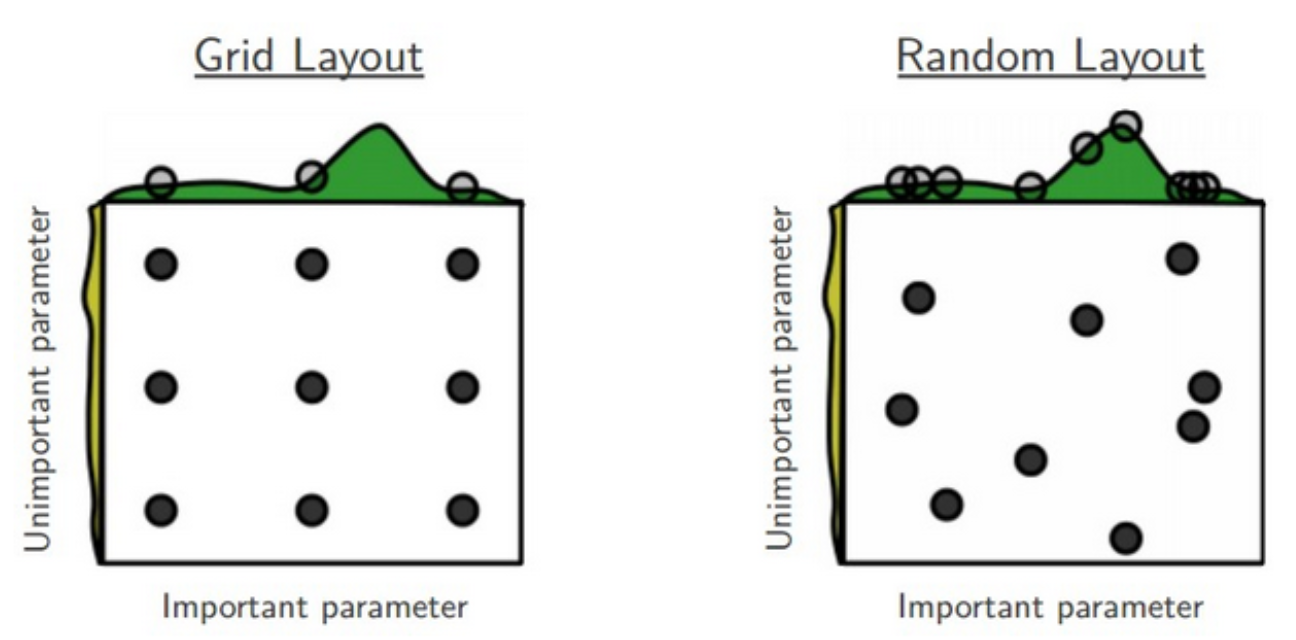
Tuning Hyper-parameters: Approaches

- DON’T optimise these numbers by looking at the test set!That is CHEATING!
- Grid search: brute-force exhaustive search among a finite set of hyper-parameter settings
- All combinations are tried, then the best setting selected
- Random search: for each hyper-parameter, define a distribution (e.g., normal, uniform)
- In the search loop, we sample randomly from these distributions
50
Double Cross-Validation
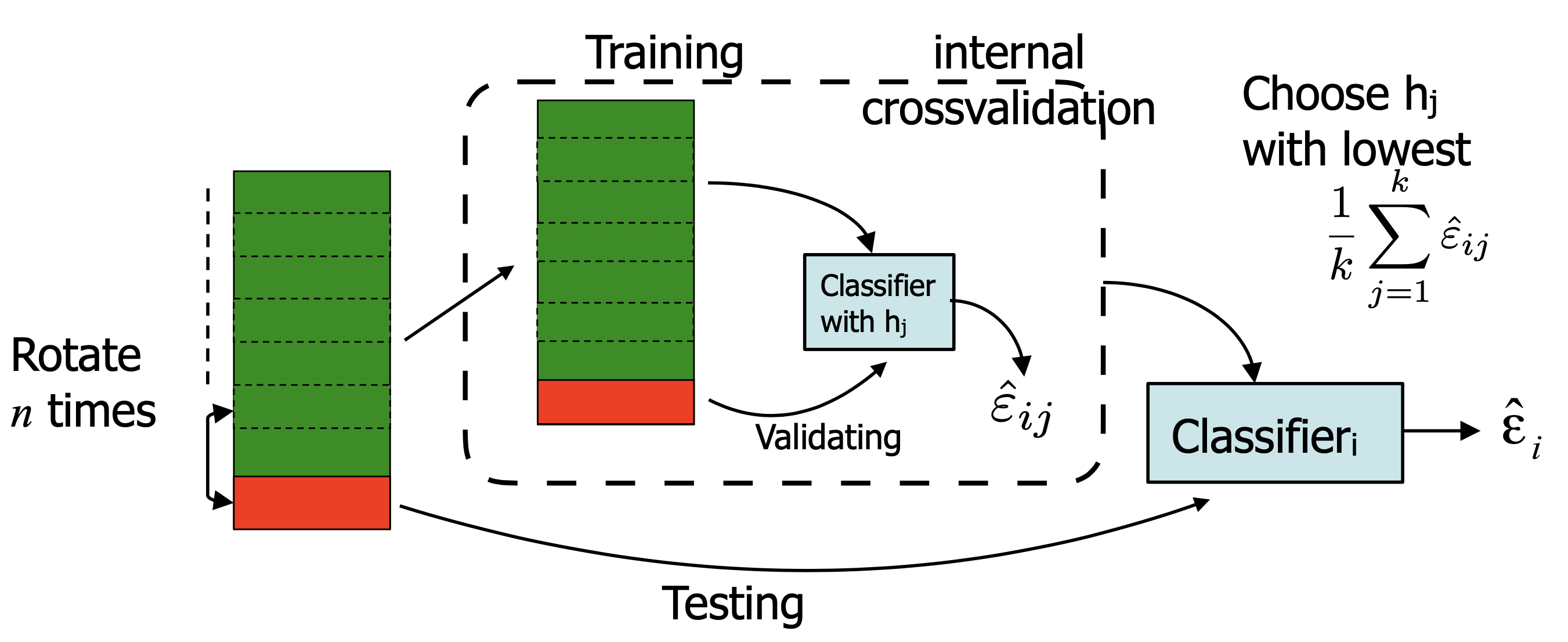
- Cross-validation inside another cross-validation
- To optimise over the hyperparameter
- The minimum error is often not the most interesting. Try to understand the advantages/disadvantages
- What errors are made? (inspect objects, inspect labels)
- What classes are problematic? (confusion matrix)
- Does adding training data help? (learning curve)
- How robust is the model?
51
Machine Learning for Design
Lecture 8
Design and Develop Machine Learning Models - Part 2
52
Credits
Grokking Machine Learning. Luis G. Serrano. Manning, 2021
[CIS 419/519 Applied Machine Learning]. Eric Eaton, Dinesh Jayaraman.
https://scikit-learn.org/stable/modules/tree.html
Deep Learning Patterns and Practices - Andrew Ferlitsch, Maanning, 2021
Machine Learning Design Patterns - Lakshmanan, Robinson, Munn, 2020