Machine Learning for Design
Lecture 5 - Part a
Training and Evaluation
Previously on ML4D
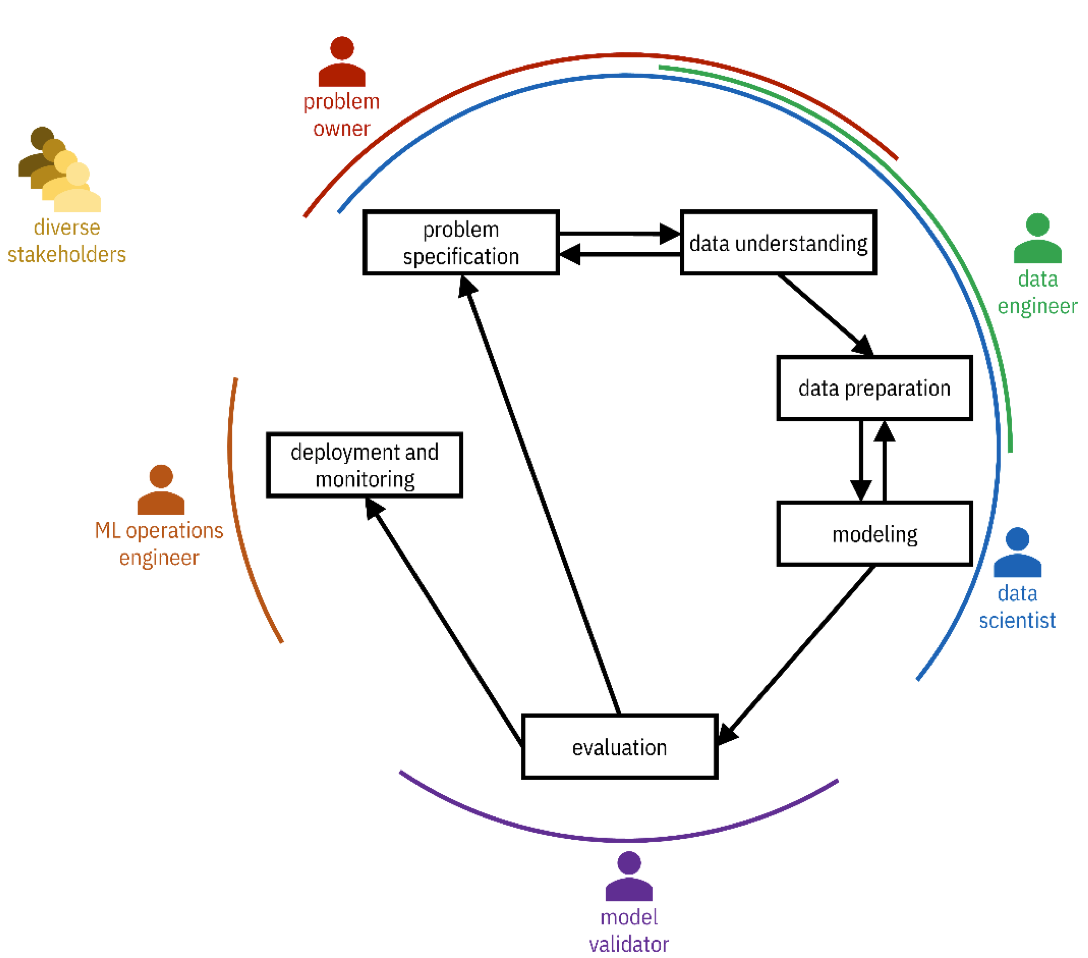
CRISP-DM Methodology
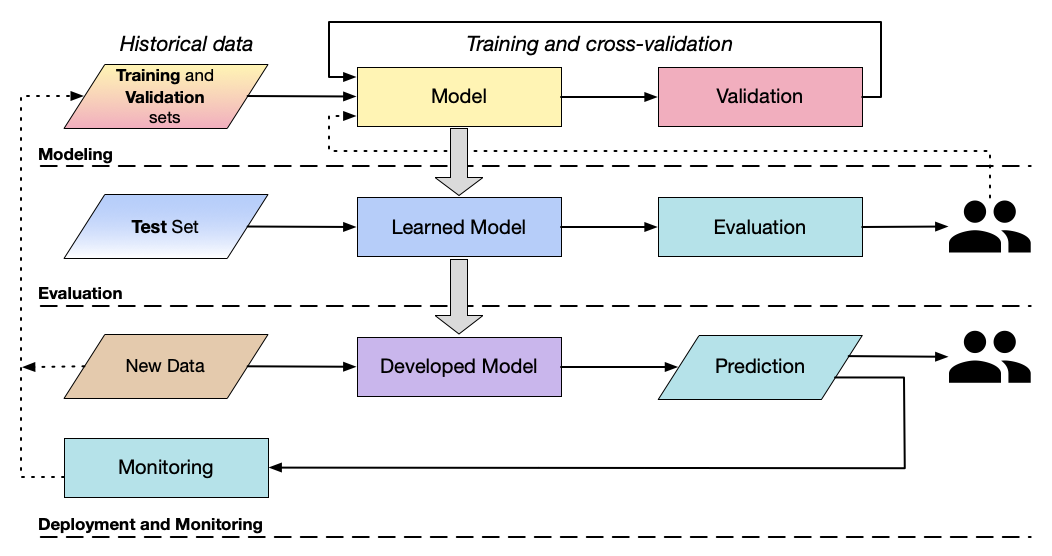
Model Development Lifecycle
Dataset Splitting
Split your data
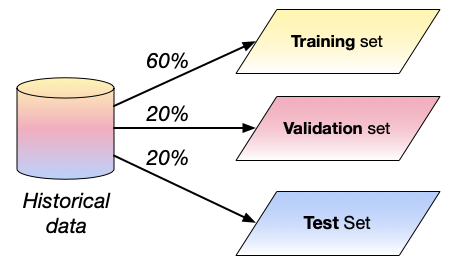
- Training set
- train
- Validation set
- fine-tune
- Test set
- evaluate
Avoid leakages

- Data items
- in the validation or evaluation sets
- Features
- highly correlated to prediction
- not present in the production environment
Cross-validation
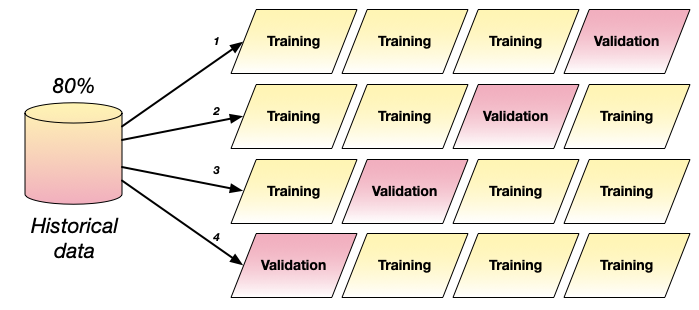
- Cycle training and validation data several times
- Useful when dataset is small
- Split the data into n portions
- Train the model n times using n−1 portions for training
- Average results
Evaluation
How to Evaluate?
- Metric
- How to measure errors?
- Both training and testing
- Training
- How to “help” the ML model to perform well?
- Validation
- How to pick the best ML model?
- Evaluation
- How to “help” the ML model to generalize?
Let errors guide you
- Errors are almost inevitable!
- How to measure errors?
- Select an evaluation procedure (a “metric”)
Model Training Process
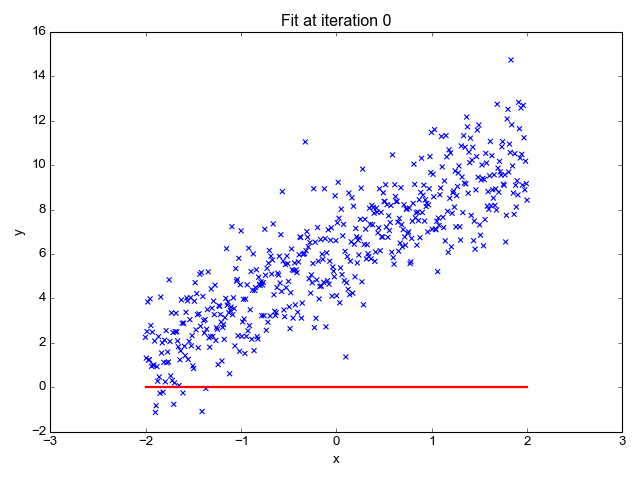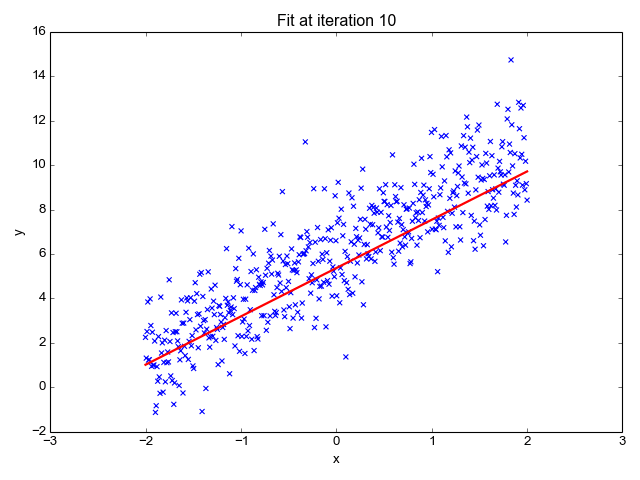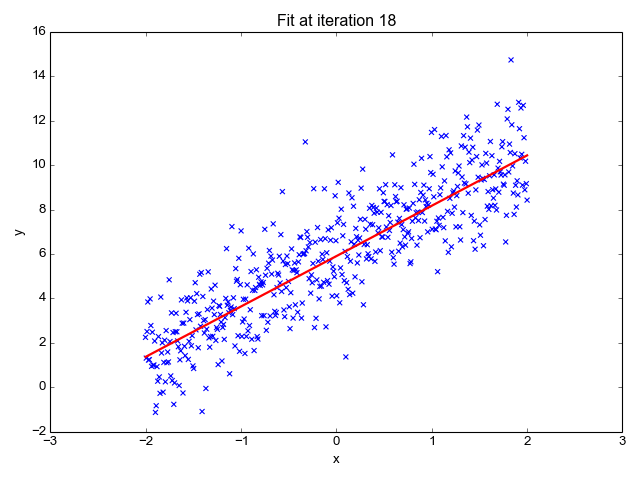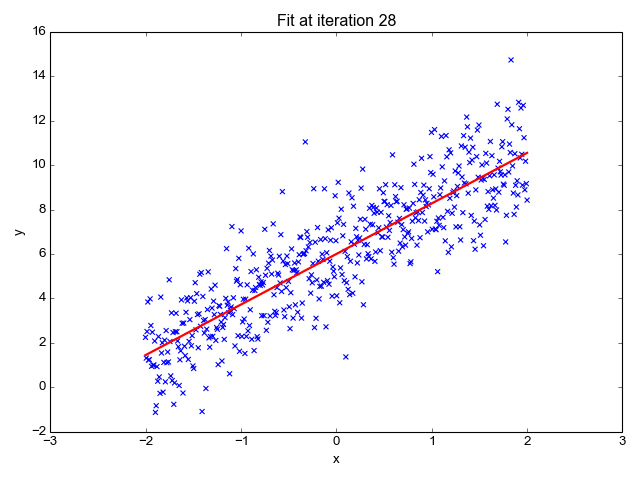
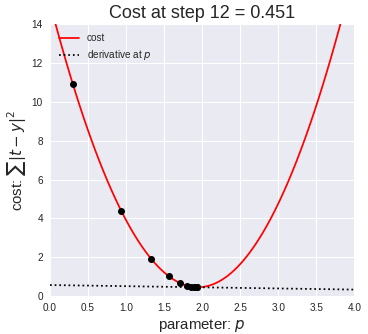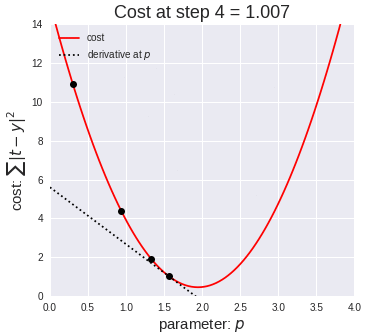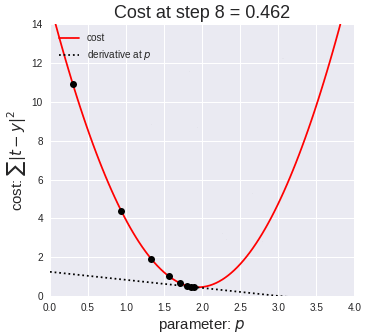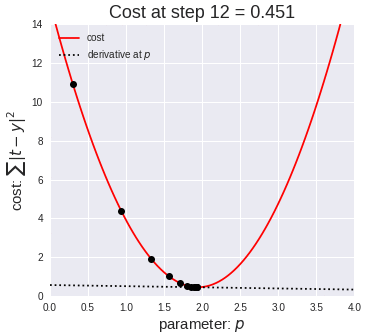
Errors
- These are the most common questions:
- How is the prediction wrong?
- How often is the prediction wrong?
- What is the cost of wrong predictions?
- How does the cost vary by the wrong prediction type?
- How can costs be minimised?
Regression
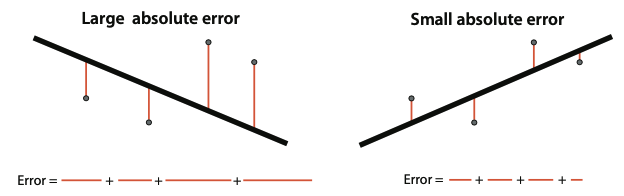
Mean absolute error
MAE=N1∑J=1N∣pj−vj∣
Average of the difference between the expected value (vj) and the predicted value (pj)
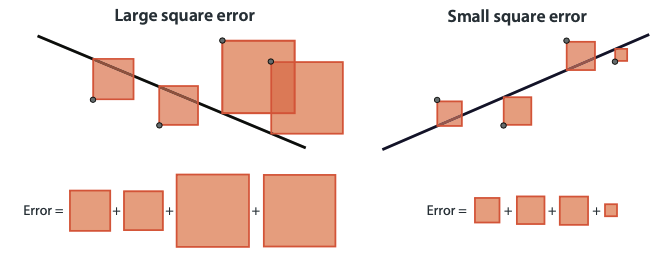
Mean square error
MSE=2N1∑J=1N(pj−vj)2
Average of the square of the difference between the training value (vj) and the expected value (pj)
Square is easier to use during the training process (derivative)
More significant errors are more pronounced
Classification
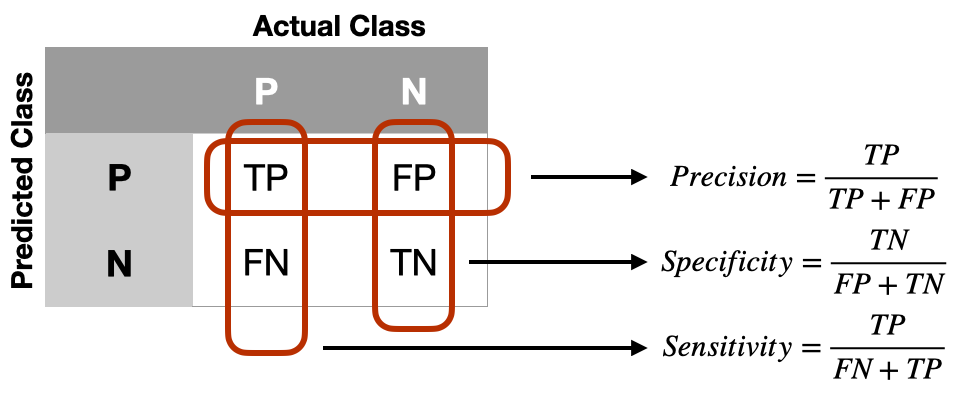
Confusion Matrix
Describes the complete performance of the model

Type I and Type II errors

Accuracy
TP+TN+FP+FNTP+TN
The percentage of times that a model is correct
The model with the highest accuracy is not necessarily the best
Some errors (e.g., False Negative) can be more costly than others
Errors are not equal


- Detecting the “Alexa” command?
- Pregnancy detection
- Cost of “false negatives”?
- Cost of “false positives”?
- Covid testing
- Cost of “false negatives”?
- Cost of “false positives”?
- Law enforcement?
Balanced Accuracy
2TP+FNTP+FP+TNTN
Average of single class performance
Good to use when the distribution of data items in classes is imbalanced
Balanced Accuracy Weighted
2(TP+FN)∗wTP+(FP+TN)∗(1−w)TN
Weighted average of single-class performance
Weight depends on the popularity of a class.
Precision
TP+FPTP
Among the examples we classified as positive, how many did we correctly classify?
Recall
TP+FNTP
Among the positive examples, how many did we correctly classify?
F1 -Score
F1=2∗P1+R11
The harmonic mean between precision and recall
What is the implicit assumption about the costs of errors?
Sensitivity (true positive rate)
FN+TPTP
Identification of the positively labeled data items
Same as recall
Specificity (false positive rate)
FP+TNTN
Identification of the negatively labeled data items
Not the same as precision
Medical Test Model
- Recall and sensitivity
- How many were correctly diagnosed as sick among the sick people (positives)?
- Precision
- Among the people diagnosed as sick, how many were sick?
- Specificity
- Among the healthy people (negatives), how many were correctly diagnosed as healthy? \u2028
Spam Detection Model
- Recall and sensitivity
- How many were correctly deleted among the spam emails (positives)?
- Precision
- Among the deleted emails, how many were spam?
- Specificity
- Among the good emails (negatives), how many were correctly sent to the inbox?\u2028
Search Engine
- Constraint: high precision
- False positives are tolerable but should be minimised
- Among the available models, pick one with a higher recall
- Metric: Recall at Precision = x%
Metrics are also designed in a multi-stakeholder context
- One team builds the mode
- Data scientists / ML engineers
- Many teams will make use of it
- e.g., product team, management team
Machine Learning for Design
Lecture 5 - Part a
Training and Evaluation
Credits
Grokking Machine Learning. Luis G. Serrano. Manning, 2021
[CIS 419/519 Applied Machine Learning]. Eric Eaton, Dinesh Jayaraman.
Deep Learning Patterns and Practices - Andrew Ferlitsch, Maanning, 2021
Machine Learning Design Patterns - Lakshmanan, Robinson, Munn, 2020